树状数组

前置知识-lowbit(）

非负整数n在二进制表示下最低位1及其后面的的0构成的数值

eg. lowbit(44) = lowbit((101100))=(100)= 4 (4的二进制表示是100）

为了求这个数值我们可以先取反

101100 => 010011 然后再加1

010011 => 010100 这时我们发现 除了最低位的1和后面的0 其余位上的数字均与原数(101100)不同 所以让两数按位与 就能得到最后的结果

因为计算机使用的是补码 所以对一个数取反加一就是负的这个数（详见wiki）

lowbit（n）=n&（~n+1）=n&-n

正题-树状数组原理

首先我们建立下图所示的森林结构，每个节点t[x]保存以x为子树中叶节点值的和

同时我们也发现，t[x]覆盖的长度就是lowbit（x），继续观察我们还会发现t[x]的父节点就是t[x+lowbit(x)]

而且整个树的深度为log₂n+1

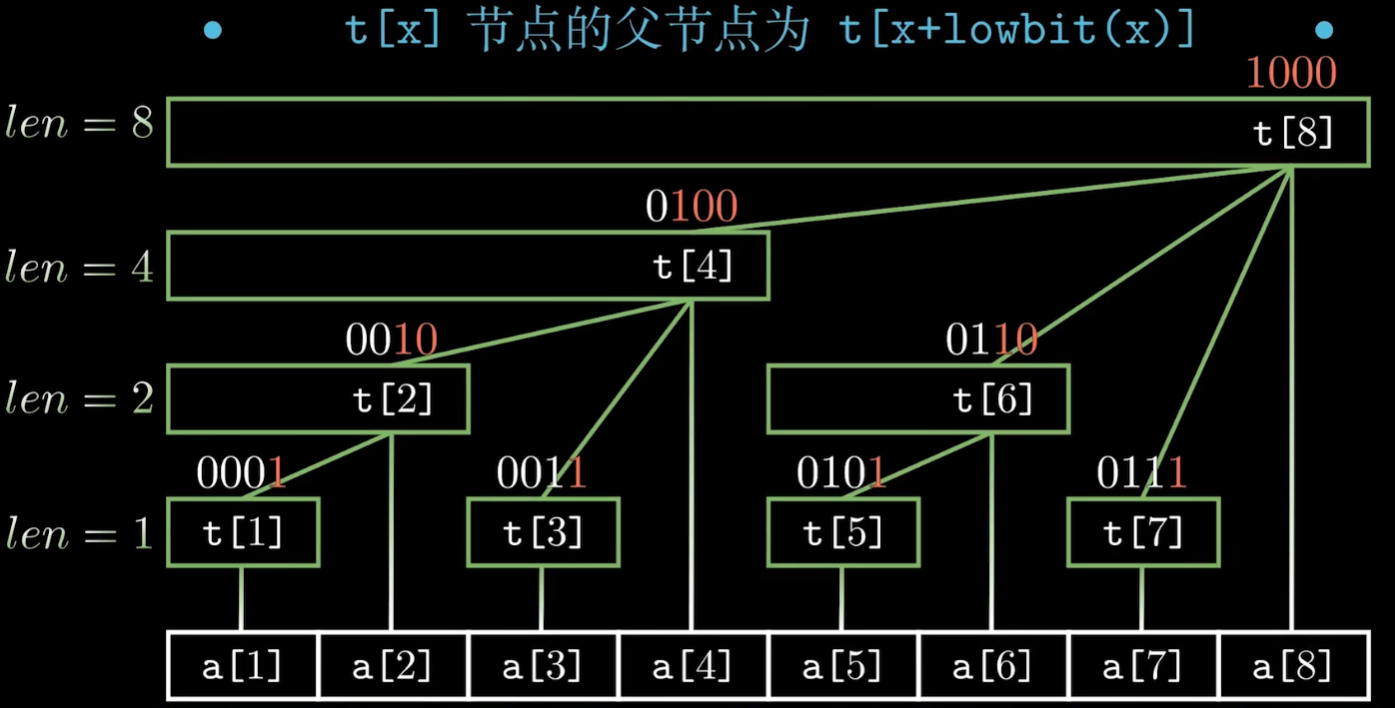
由此，我们能很容易得到对应操作的代码:

add(x,k)操作（t[x]+k）-单点修改

在整棵树上维护这个值，需要一层一层向上找到父节点，并按照需要依次+k

1
2
3
4

void add(int x,int k)
{
for(;x<=n;x+=x&-x) t[x]+=k;
}

add(x)操作 （查询t[x]的前缀和）-区间查询

计算这个值的时候，我们只需要依次累加其左上节点的和即可

我们发现这个所谓“左上”节点正是t[x-lowbit(x)]

1
2
3
4
5
6

int ask(int x)
{
   int ans=0;
   for(;x;x-=x&-x) ans+=t[x]
   return ans;
}

下面贴一个例题

add(x,y,k)操作- 区间修改

对于区间修改我们要引入一个新的概念——差分数组

假如原数组为 3 1 2 4 2 1 3

那他的差分数组就是3 -2 1 2 -2 -1 2

就是原数减去它前面的数，特别的第一个数减去0即可

差分数组有一个性质是差分数组的前缀和就是原数组

同理，前缀和数组的差分数组就是原数组

言归正传，如果要进行区间修改操作，我们不能对原数组指定范围内依次修改，因为太繁琐了，所以我们可以维护一个差分数组b，如果在（r,l）范围内进行加k操作，对于数组b，我们只需要b[r]+k,b[l+1]-k 即可。因为r到l范围内都加了k的话，除了两端的差有改变，其他差是不会改变的—— (a+c)-(b+c)=a-b

这样，我们就巧妙地完成了将区间修改转变为单点修改的转化，然后就同理add(x,k)操作喽

在此条件下还会引申出单点查询的操作

对于差分数组b我们想要得到原数组的某一个值，我们求其前缀和即可，（前面的性质提到了）同理add(x)操作

P3374 树状数组1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 x
• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 x 个数加上 k
• 2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1复制

1
2
3
4
5
6
7

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1复制

1
2

14
16

说明/提示

【数据范围】

对于 30% 的数据，1≤n≤8，1≤m≤10；
对于 70% 的数据，1≤n,m≤104；
对于 100% 的数据，1≤n,m≤5×105。

数据保证对于任意时刻，a 的任意子区间（包括长度为 1 和 n 的子区间）和均在 [−231**,231**) 范围内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cmath>
 #include <cstring>
 using namespace std;
 int n,m,t[2000010];
 void add(int x,int k)
{
    for(;x<=n;x+=x&-x) t[x]+=k;
}
int sum(int x)
{
  int ans=0;
  for(;x;x-=x&-x) ans+=t[x];
  return ans;
}
 int main()
 {
     cin>>n>>m;
     for(int i=1;i<=n;i++)
     {
         int a;
         cin>>a;
         add(i,a);
     }
     for(int i=1;i<=m;i++)
     {
         int a,b,c;
         cin>>a>>b>>c;
         if(a==1)
             add(b,c);
         if(a==2)
             cout<<sum(c)-sum(b-1)<<endl;
     }
 }

P3368 树状数组2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 x；
2. 求出某一个数的值。

输入格式

第一行包含两个整数 N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含 N 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 M 行每行包含 2 或 4个整数，表示一个操作，具体如下：

操作 1： 格式：1 x y k 含义：将区间 [x,y] 内每个数加上 k；

操作 2： 格式：2 x 含义：输出第 x 个数的值。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1复制

1
2
3
4
5
6
7

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出 #1复制

1
2

6
10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include<bits/stdc++.h>
 using namespace std;
 int n,m,t[2000001]={0};
 void add(int x,int k)
{
    for(;x<=n;x+=x&-x) t[x]+=k;
}
int sum(int x)
{
  int ans=0;
  for(;x;x-=x&-x) ans+=t[x];
  return ans;
}
 int main()
 {
     ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
     cin>>n>>m;
     int q=0;
     for(int i=1;i<=n;i++)
     {
         int a;
         cin>>a;
         add(i,a-q);
         q=a;
     }
     for(int i=1;i<=m;i++)
     {
         int a,b,c,d;
         cin>>a;
         if(a==1)
         {
            cin>>b>>c>>d;
            add(b,d); 
            add(c+1,-d);
         }
   
         if(a==2)
         {
             cin>>c;
             cout<<sum(c)<<'\n';
         }  
     }
     return 0;
 }